hash, trie, kmp, manacher
字符串Hash 对于给定的字符串,通过设计函数将其映射到另一个集合上的方法,称为hash
我们希望 尽可能少的发生hash冲突/碰撞(两个不同字符串的映射值一样),值域保证冲突率小的同时尽可能低
平铺直叙太多抽象内容也不利于理解,直接看实际问题比较好
映射到集合,区分不同的字符串 洛谷 P3370 【模板】字符串哈希
考虑一种暴力做法,排序后去重,容易发现字符串一旦涉及到比较,代价都会比较大
这里如果写个快排,比较的时间复杂度不容忽视,整体会到$O(N\log{N}M)$的程度,这显然炸了
考虑$O(NM)$建立字符串到数值的映射,这样在排序、去重的时候就排除了比较的复杂度
#include <algorithm> #include <iostream> #include <set> #include <string> #include <vector> int main () std::vector<int > v; std::string s; int n; std::cin >> n; auto hash = [&](std::string& x) { int ans = 0 ; for (char c : x) { ans *= 10 ; ans += c - 'a' ; } v.push_back (ans); }; for (int i = 1 ; i <= n; ++i) { std::cin >> s; hash (s); } sort (v.begin (), v.end ()); std::cout << std::unique (v.begin (), v.end ()) - v.begin (); return 0 ; }
如上所示,这就是一个字符串hash
考虑直接把字符串映射成一个26进制的数(当然以10进制保存),然后去重即可
当然这种方式产生的值域太大,并不是一个好的hash,但如果取模数,就会碰到hash冲突,因此设计一个好的hash是难点
其他要用到hash的地方一般题目不会太简单,到时单独列举。
Trie 懒得画图了,不如直接看OI-wiki
trie是一个DAG,字符作为边,即转移的依据
一个简单的例子
P2580 于是他错误的点名开始了
#include <bits/stdc++.h> using namespace std;const int N=500010 ;int ch[N][30 ],tag[N],tot;void insert (string& s) int p=0 ; for (char _c:s){ int c=_c-'a' ; if (!ch[p][c]) ch[p][c]=++tot; p=ch[p][c]; } tag[p]=1 ; } int main () int n,m;cin>>n; for (int i=0 ;i<n;++i){ string s;cin>>s; insert (s); } cin>>m; for (int i=0 ;i<m;++i){ int p=0 ; string s; cin>>s; for (char _c:s){ int c=_c-'a' ; if (!ch[p][c]) break ; p=ch[p][c]; } if (tag[p]==1 ) tag[p]=2 ,puts ("OK" ); else if (tag[p]==2 ) puts ("REPEAT" ); else puts ("WRONG" ); } return 0 ; }
KMP KMP可以在线性时间内判定字符串$A_{1..n}$是否为字符串$B_{1..m}$的子串,并求出字符串$A$在字符串$B$中每次出现的位置
构造next数组 对模式串$A$进行自我匹配 定义
$next_i=\max{j\mid j < i, A_{i-j+1..i} = A_{1..j}}$
即对于子串$A_{1…i}$,其前后缀匹配的最大长度
记住这个集合${j}$,之后会多次用到
易知 $next_1=0$
引理: 如果$j_0$是集合$j$里面的一个元素 那么小于$j_0$的最大的元素就是next[$j_0$]
若要找到${j}$中小于$j_0$的最大元素
即对于$A[i-j_0+1 \sim i] = A[1 \sim j_0]$,要得到最大的$j_1$
满足$A[i-j_1+1 \sim i] = A[1 \sim j_1]$ 且 $j_1<j_0$
则发现 $A[j_0-j_1+1+1\sim j_0]=A[i-j_1+1\sim i]=A[1\sim j_1]$
不难发现对于$A_{1…j_0}$,前$j_1$和后$j_1$是相同的,并且这个$j_1$定义最大
引理求解next 若$j_0\in next_i$的${j}$,则 $j_0-1\in next_{i-1}$的${j}$
反之对于 $next_i$,$next_{i-1}+1,next_{next_{i-1}}+1,\cdots$都可以作为候选项
其实就是利用引理加速筛选可能的匹配,而每次恰好都是最大值作为候选项
求模式串的next std::string A; std::cin >> A; int n=int (A.size ());std::vector<int > nxt (n+1 ) ;nxt[1 ] = 0 ; for (int i = 2 , j = 0 ; i <= n; ++i) { while (j > 0 && A[i] != A[j + 1 ]) j = nxt[j]; if (A[i] == A[j + 1 ]) ++j; nxt[i] = j; }
匹配目标串 对模式串$A$和目标串$B$进行匹配
得到$A$的$next$后,考虑$A+B$,不难发现,如果在找这个串的$next$时,若某一位置上有$next_i=len(A)$且$i\geq n+m$时,其实就是一次A在B中的出现被匹配到
即 $next_i={j\mid A+B[len_A+i-j+1\sim len_A+len_B]=A+B[1\sim j],j=n}$
最大的$j$也就是$n$了,所以转移用的$next_i$完全可以用A的
这种利用失配指针的思想在AC自动机中也会出现
发现可以去掉拼在前面的$A$,并没有什么影响
即考虑
$f_i = max{j\mid j < i, B[i-j+1 \sim i] = A[1 \sim j]}$
当$f_i=n$时,就在$B$中找到了$A$的出现位置
for (int i = 1 , j = 0 ; i <= m; i++) { while (j > 0 && target[i] != pattern[j+1 ]) j=nxt[j]; if (target[i]==pattern[j+1 ]) j++; if (j == n) { } }
#include <iostream> #include <string> #include <vector> int main () std::string a, b; std::cin >> a >> b; int n = a.size (), m = b.size (); a = '$' + a, b = '$' + b; std::vector nxt (m + 1 , 0 ) ; for (int i = 2 , j = 0 ; i <= m; ++i) { while (j > 0 && b[j + 1 ] != b[i]) j = nxt[j]; if (b[j + 1 ] == b[i]) ++j; nxt[i] = j; } for (int i = 1 , j = 0 ; i <= n; ++i) { while (j > 0 && a[i] != b[j + 1 ]) j = nxt[j]; if (a[i] == b[j + 1 ]) ++j; if (j == m) std::cout << i - m + 1 << '\n' ; } for (int i = 1 ; i <= m; ++i) std::cout << nxt[i] << " \0" [i == m]; return 0 ; }
观察一下 发现整个过程j=nxt[j]的变化幅度不超过j增加的幅度总和
j每次循环至多增加1 所以时间复杂度复杂度为$O(N+M)$ 空间复杂度为$O(N)$
水B站的时候发现的,ylq的最爱
回文串问题 给定长为$n$的字符串$s$,找出所有对$(i,j)$使得$s_{i..j}$是一个回文串
用一种不同于确定起点和终点位置来找回文串的方式来描述,考虑维护一个$d_1[i]$和$d_2[i]$
$d_1[i]$表示以位置i为中心的,长度为奇数的回文串个数,事实上也维护了回文串的长度,因为回文串掐头去尾还是回文的
$d_2[i]$同理,长为偶数的回文串个数。
$d_1[i]$和$d_2[i]$均为位置$i$到最长的回文串右端所包含的字符个数
朴素的维护 $d_1[i]$,$d_2[i]$同理,下文忽略$d_2$
std::string s; std::cin >> s; int n = s.size ();std::vector<int > d1 (n) , d2 (n) ;for (int i = 0 ; i < n; ++i) { d1[i] = 1 ; while (0 <= i - d1[i] && i + d1[i] < n && s[i - d1[i]] == s[i + d1[i]]) d1[i]++; d2[i] = 0 ; while (0 <= i - d2[i] - 1 && i + d2[i] < n && s[i - d2[i] - 1 ] == s[i + d2[i]]) d2[i]++; }
Manacher 过程 维护一个最靠右的回文串$(l,r)$(即具有最大的$r$)
考虑$d_1[i]$,且之前的$d_1[]$都计算完了,分类讨论
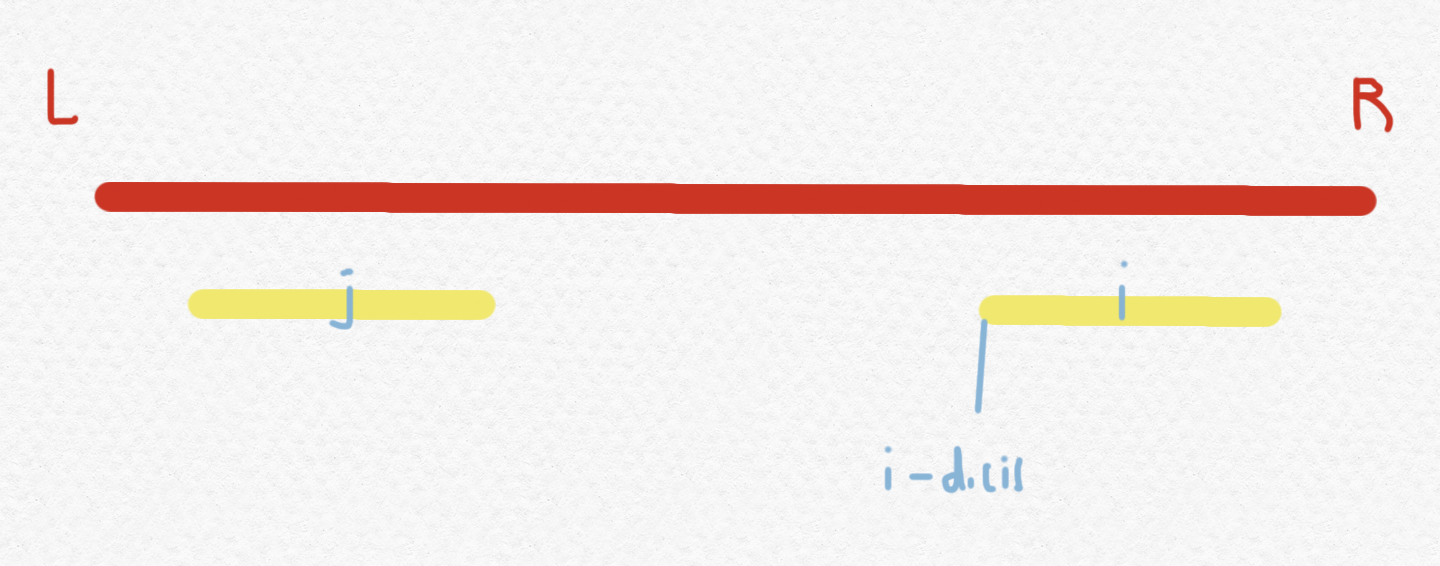
考虑利用已经维护好了的$d_1[]$,找到$(l,r)$中$i$对称的位置$j=l+(r-i)$,那么如下图,对应的黄色区域一定是相同的,即$d_1[i]=d_1[j]$,当然也有例外情况,就是黄色区域跑出了红色区域的时候,这个时候我们要截断$d_1[i]$,令其最大为$r-i$,但是反过来,$j$是否可能会在$i$右边,导致截断的时候去往左边考虑?答案是否定的,因为这样的话$(l,r)$就不是最靠右的了
$d_2[]$的情况类似,当然因为偶数长度所以边界拿的时候写法改一下即可。同时更新一个$(l,r)$即可。
复杂度分析 这个没啥好看的,每次r都会扩展至少1的长度,均摊$O(N)$
#include <algorithm> #include <iostream> #include <string> #include <vector> int main () std::string s; std::cin >> s; int n = s.size (); std::vector<int > d1 (n) , d2 (n) ; int ans = 0 ; for (int i = 0 , l = 0 , r = -1 ; i < n; ++i) { int k = (i > r) ? 1 : std::min (d1[l + r - i], r - i + 1 ); while (0 <= i - k && i + k < n && s[i - k] == s[i + k]) ++k; d1[i] = k--; ans = std::max (ans, d1[i] * 2 - 1 ); if (i + k > r) l = i - k, r = i + k; } for (int i = 0 , l = 0 , r = -1 ; i < n; ++i) { int k = (i > r) ? 0 : std::min (d2[r + l - i + 1 ], r - i + 1 ); while (0 <= i - k - 1 && i + k < n && s[i - k - 1 ] == s[i + k]) ++k; d2[i] = k--; ans = std::max (ans, d2[i] * 2 ); if (i + k > r) { l = i - k - 1 ; r = i + k; } } std::cout << ans; return 0 ; }